Merhaba
Crypto 101 yazı serisinin 4. bölümüne hoşgeldiniz.
Stream Ciphers
Stream Cipher konusu normal şartlarda Block Cipher konusundan önce ele alınarak anlatılmaktadır. Benim bu konuyu sona bırakma sebebim ise anlaşılması ve odaklanması daha zor olan Block Ciphers konusundan sonra “araya bir çerez” konu koyarak siz okurları peş peşe zor konular ile sıkıştırmamış olmaktır.
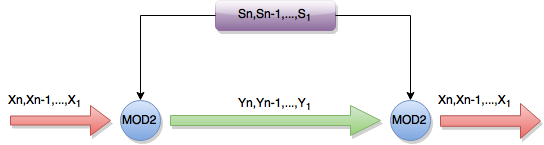
Stream kelimesi Türkçe’mizde “akış, dere, akım” anlamlarına gelmektedir ve aşağıdaki şekilde ifade edilen akış diagramı vardır.
Encryption Yi = e(Xi) = (Xi + Si)MOD2
Decryption Xi = d(Yi) = (Yi + Si)MOD2
Bu denklere bakıldığında akla gelen ilk soru Encryption ve Decryption işlemlerinde neden toplama işleminin yapıldığı ? olacaktır. Normal şartlarda şifreleme işleminde toplama işlemi yapıldıysa deşifreleme işleminde çıkartma yapılması beklenirdi. Bu sorunun cevabı son derece basit bir moduler aritmatik bilgisinde saklıdır.
MOD 2 işleminde toplama ve çıkartma aynı işlemdir.
Yani özet olarak isterseniz Decryption işleminde toplama yerine çıkartma da yapabilirsiniz. Bu soruya cevap verdikten sonra akla gelebilecek ikinci soruyu ele alalım, “Daha önce ki yazılarınızda XOR bu tür işlerin kalbi olacağını söylediniz. Peki neden tamda XOR kullanılabilecek bir yerde Mod 2 işlemi yapıldı ?”
Bu güzel soruya ikili sistemde Mod 2 işleminin doğrulama tablosunu analiz ederek cevap verebiliriz.
Xi Si | Yi (mod2) ------------ 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0
Bu tablonun girişleri Xi ve Si yani Plain-text ve Key olarak belirlenmiş durumdadır. Çıkış olarak ise Cipher-text yani Yi bitleri gözükmektedir. Tabloya genel olarak baktığımızda aslında çok yakından tanıdığımız XOR kapısı ile bire bir aynıdır.
Random Number Generation (RNG)
Random Number Generation, bilgisayar sistemleri ile gerçek rastsal sayı oluşturabilme çözümlerini ele almaktadır. Günlük hayatta bir birey olarak rastgele sayı üretmek çok zor değildir, örneğin “7272621515183949317484959” buyrun size rastgele tuşlara basarak ürettiğim bir sayı. Biz insanlar için son derece kolay bir işlem olan rastgele sayı üretme işlemini bilgisayar sistemlerine nasıl yaptırabiliriz ? sorusu ciddi bir sorudur ve doğru bir cevabı hak etmektedir. Zaten bilgisayarın aklı yoktur ki “aklından 1000 basamaklı bir sayı söyle ?” sorusuna cevap versin.
Bu başlık aşağıdaki 3 ana alt başlık ile işlenecektir.
a) True Random Number Generator ( TRNG)
Bozuk para ile yapacağınız yazı-tura yani 1 ve 0 işleminde sırasıyla gelen 1 ve 0’ları peşpeşe kullanarak gerçekten bir TRNG elde edebilirsiniz. Tahmin edebildiğiniz üzere bu işlem uygulanabilirlik açısında son derece zordur. Bu nedenle genellikle sadece 1 defalık üretilecek son derece önemli anahtarlar için kullanılmaktadır. Örneğin https://www.bitaddress.org adresi, mouse hareketlerinizin koordinatlarını kaynak olarak kullanarak bitcoin adresi üretmektedir. Saldırganları bir kenara bırakırsak, kendi kendinize iki kere aynı adresi üretmeniz bile neredeyse imkansızdır.
b) Pseudo Random Number Generator (PRNG)
Matematiksel bir fonksiyon ile bilgisayar sistemleri tarafından üretilen rastgele sayırlardır. Fiziksel sistemler üzerinden elde edilen TRNG’e göre gerçek rastgelelik ortadan kalktığı için (matematiksel fonksiyon ile hesaplanan bir değer oluşundan ötürü) adı Pseudo yani sözde rastgele sayı olarak belirlenmiştir.
Çoğu programlama dilinin rastgele sayı üretme fonksiyonu PRNG sistemdir ve bu fonksiyonlar doğrudan matematiksel bir “fonksiyonun” implementasyonlarıdır. Örneğin basit bir matematiksel denklemi ve denklemin python implementasyonunu birlikte gerçekleştirelim.
Xi+1 = (aXi + c) mod M ve i=0,1,2,3… olarak devam eden bir sıralı dizi olduğunu kabul edelim. Ri kümesi ile ürettiğimiz rastgele sayırları ifade etsin. Son işlem olarak olarak, hesaplanan Xi değerleri M sayısına bölünerek Ri’ler elde edilecektir. Ri = Xi / M
X0=130, a=5, c=37, M=100 olsun. Bu değerler bir dizi rastgele sayı üretmek için başlangıç değerlerimizdir. Bu durumda denklemin başlangıç değerleri ile birlikte iterasyonu aşağıdaki gibi olacaktır.
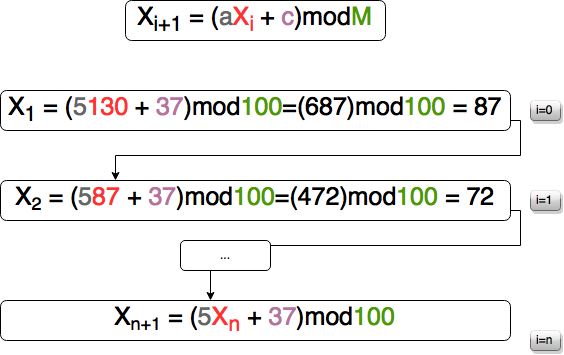
Yukarıda ki şekilde görüşdüğü üzere N tane sayıda üretilmiş değerden Ri rastgele sayılarımızı hesaplamak için son bir işlem kaldı. Oda Ri = Xi / M yani tüm değerleri 100 olan M değerine bölmek.
R1 = 87/100 = 0.87
R2 = 72/100 = 0.72
…
Rn = Xn/100
şeklinde hesaplanacaktır. Bu matematiksel fonksiyonun python implementasyonu ise aşağıdaki şekilde yapılabilir.
#!/usr/bin/env python
from __future__ import division
"""
Thi is very basic LCG function.
Xi+1 = (aXi + c) mod M ve i=0,1,2,3
Ri= Xi/M
You are free to select random values for xZero, a, c and Mod variables.
xZero is our initialization vector.
"""
class LCG(object):
def __init__(self, iv):
self.xZero = iv
def generate(self):
a = 7**7 # Value is = 823543
c = 5**10 # Value is = 9765625
mod = 2**24
self.xZero = (a * self.xZero + c) % mod
return self.xZero / mod
feed = LCG(1826618237451) # Random Number
for i in range(10):
print feed.generate()
Sonuçlara baktığımızda, basit ihtiyaçlar için kullanabileceğimiz, kesinlikle herhangi bir şifreleme işleminde kullanılmaması gereken bize özgü rastgele sayılarımızın oluştuğu gözlemlenebilir.
➜ 4-stream_ciphers_prng git:(master) ✗ python prng.py 0.249200224876 0.682871997356 0.0353955030441 0.300840079784 0.323902487755 0.208549678326 0.209813952446 0.393915832043 0.208144545555 0.565556704998